physics – Notes on Disordered Matter

How to see the temperature dependence of the open-circuit voltage from the ideal diode equation?

The open-circuit voltage is the voltage in the current–voltage characteristics of a solar cell that is defined where the current is zero. That means that the (internal) charge carrier generation and recombination rates are equal, so that no net current can flow out of the device.

We can simply rearrange the ideal diode equation and solve for the open-circuit voltage. The ideal diode equation was discussed with respect to the ideality factor in this post. The current density is given as

$j(V)=j_0 \left(\exp\left(\frac{eV}{n_{id}kT}\right)-1\right) - j_\text{gen}$ ,

with $V$ the voltage, $e$ elementary charge, $kT$ thermal voltage, $n_\mathrm{id}$ the recombination ideality factor, $j_0$ the dark saturation current, and $j_\mathrm{gen}$ the photogenerated current. For simplicity, the latter is chosen to be voltage independent, and therefore is equal to the short-circuit current $j_\mathrm{sc}$ .

As the open-circuit voltage is determined at zero net current, $j(V_\mathrm{oc}) = 0$ , we get

$j(V_\mathrm{oc}) = 0 = j_0 \left(\exp\left(\frac{eV_\mathrm{oc}}{n_{id}kT}\right)-1\right) - j_\text{gen}$ ,

which we can rearrange to yield the open-circuit voltage

$V_\mathrm{oc} = \frac{n_{id}kT}{e} \ln \left( \frac{j_\text{gen} + j_0}{j_0} \right)$ .

Here, $j_\text{gen}$ is the photocurrent due to solar illumination, and the dark saturation current density $j_0$ is due to excitation of thermal “black body” photons from the ambient at, say, room temperature. In the simplest case – in the dark where $j_\text{gen} = 0$ – we see that $V_\mathrm{oc} = 0$ , too. Generally, the thermal generation leading to $j_0$ is much weaker than the solar generation $j_\text{gen}$ , therefore

$V_\mathrm{oc} \approx \frac{n_{id}kT}{e} \ln \left( \frac{j_\text{gen}}{j_0} \right)$ .

is usually a very good approximation.

This simple equation to describe the open-circuit voltage is very general and can describe (outside of the shunt region, which is not considered here) very different solar cell technologies correctly. The reason is that many parameters that differ for different semiconductors are accounted for. So what determines the open-circuit voltage?

At a given temperature, the open circuit voltage is determined by
– $j_\text{gen}$ ,
– $j_0$ , and
– $n_\text{id}$ (which was discussed previously)..

The generation current density

$j_\text{gen} = e \int EQE(E)\, b_s(E)\, dE,$

which means it is given by how much of the solar photon flux of the sun, $b_s$ , is converted into electrons – which is described by the external quantum efficiency $EQE(E)$ . The $EQE$ includes reflection losses, the absorptance (in the simplest case 0 below the bandgap and 1 for energies at or higher than the band gap $E_g$ ), and charge collection losses (for instance due to the transport resistance). Essentially, the higher the bandgap $E_g$ , the higher $j_\text{gen}$ – which leads to a higher open-circuit voltage.

The dark saturation current density in an ideal solar cell without non-radiative losses is essentially given by

$j_0 = e \int EQE(E)\, b_a(E)\, dE.$

The only difference to the equation for $j_\text{gen}$ is that the photons do not come from the sun anymore, but from the ambient (note the subscript a;). This $b_a(E)$ is just Planck’s law to describe thermal radiation from black bodies, so everything “earthly” around the solar cell that emits at the current temperature $T$ (or $T_a$ , the temperature of the ambient). While the sun that generates $j_\text{gen}$ can also be well approximated by a block body and Planck’s law – assuming a black body temperature of the sun of $T_s \approx 5800 \text{ K}$ , usually the temperature of the ambient that leads to $j_0$ corresponds to the solar cell temperature… for instance, $T = T_a \approx 300 \text{ K}$ .

With this in mind, we can maybe see already what determines the temperature dependence of the open-circuit voltage! In

$V_\mathrm{oc}(T) \approx \frac{n_{id}(T)kT}{e} \ln \left( \frac{j_\text{gen}}{j_0(T)} \right)$ ,

there is an explicit temperature dependence in the prefactor, $kT$ , which “promises” increasing open-circuit voltages at higher temperatures, but from measurements we know that the opposite happens: the open-circuit voltage increases towards lower temperatures!

Except for temperature-dependent changes in the charge collection (or bandgap), $j_\text{gen}$ is (solar cell) temperature independent. The ideality factor can depend on temperature (and, in organic solar cells, even light intensity dependence [Saladina 2023]), but does not dominate the temperature dependence of $V_\mathrm{oc}$ . The real “culprit” is indeed the very important dark saturation current density $j_0$ , which describes charge carrier generation (and recombination!) across the bandgap by thermal photons (plus, in real systems, non-radiative processes)!

When we approximate the equation for the ideal dark saturation current density (ideal, because we again neglect non-radiative losses) from above – using the Boltzmann approximation instead of the Bose-Einstein statistics that are featured in Planck’s law – we can describe the temperature dependence of $j_0$ :

$j_0(T) \approx j_{00} \exp \left( - \frac{E_g}{n(T)kT} \right) \qquad \mathrm{(*)}$ .

The temperature here is, again, the solar cell’s and the ambient temperature is equal to it. We assume for simplicity (again a pretty good approximation) that the bandgap $E_g$ is not (or only very weakly) temperature dependent. The prefactor $j_{00}$ is essentially the dark saturation current density at infinite temperature, when the effective density of states is (hypothetically) completely filled, which is reduced by lower temperatures: the thermal photons from the ambient generate electron–hole pairs across the bandgap, increasing $j_0$ and – as it is in the denominator of the equation for $V_\mathrm{oc}$ – decreasing the open-circuit voltage at higher temperatures. We can make this result more transparent when entering the temperature dependent dark saturation current density into the equation for the open-circuit voltage: (For simplicitly, I left the explicit temperature dependence of the ideality factor out, writing $n_{id}$ instead of $n_{id}(T)$ .)

$V_\mathrm{oc}(T) \approx \frac{n_{id}kT}{e} \ln \left( \frac{j_\text{gen}}{j_{00} \exp \left( - \frac{E_g}{n_{id}kT} \right)} \right)$
$= \frac{n_{id}kT}{e} \ln \left( \frac{j_\text{gen}}{j_{00}} \exp \left(\frac{E_g}{n_{id}kT} \right) \right)$
$= \frac{n_{id}kT}{e} \ln \left( \exp \left(\frac{E_g}{n_{id}kT} \right) \right) + \frac{n_{id}kT}{e} \ln \left( \frac{j_\text{gen}}{j_{00}} \right)$
$= \frac{n_{id}kT}{e} \frac{E_g}{n_{id}kT} + \frac{n_{id}kT}{e} \ln \left( \frac{j_\text{gen}}{j_{00}} \right)$
$= \frac{E_g}{e} + \frac{n_{id}kT}{e} \ln \left( \frac{j_\text{gen}}{j_{00}} \right)$

We see now that the maximum open circuit voltage at zero temperature (in a system described by classical Boltzmann approximation, Voc(T) for a-Si H solar cell. i.e. without the energetic disorder that is an important topic in organic solar cells) is given by the (effective) bandgap of the device – usually the bandgap of the active layer material. The open-circuit voltage is reduced at higher temperatures(!) despite the plus sign after the term $E_g/e$ : the dark saturation current density at infinite temperature $j_{00}$ is larger than $j_\mathrm{gen}$ , and the argument of a natural logarithm with argument smaller than one is negative. This means that the second term on the right-hand side is negative, and $V_\mathrm{oc}$ decreases at higher temperatures.

I’ll leave it here for now, with two comments: first, there is more to be said about why one always should use the ideality factor in the equation $\mathrm{(*)}$ that gives the temperature dependence of the dark saturation current density! And second, the impact of energetic disorder on $V_\mathrm{oc}$ is very important and leads to changes – the devil in the details;)

Pitfalls when measuring recombination lifetimes in organic solar cells

Six years ago, I came across an interesting publication by David Kiermasch and Kristofer Tvingstedt, [Kiermasch et al 2018], titled Revisiting lifetimes from transient electrical characterization of thin film solar cells; a capacitive concern evaluated for silicon, organic and perovskite devices. It shows that particular in thin film solar cells, the time constant determined by voltage based techniques – open circuit voltage decay (OCVD), transient photovoltage (TPV), intensity modulated photovoltage spectroscopy (IMVS) – is in many cases not the recombination lifetime, but corresponds to an RC-time from the device itself. While the authors did not find this effect, they showed impressively how most modern solar cells are limited in this respect, and it has to be verified carefully whether or not the experimentally determined time constants do correspond to recombination lifetimes!

I took this publication very seriously. Below I show you a summary slide I made for my group seminar in the year of publication, 2018.

Carstens tuesday note 2018.

The shown equation was actually animated, sorry for making your life harder (but mine easier;). Briefly, the idea of why an RC limitation shows up is the following. The charge in the device $Q$ is changing with time during the measurement – no matter if the method is a large signal (OCVD) or small signal method (TPC, IMVS):

$\frac{dQ(t)}{dt} = \underbrace{\frac{dQ(t)}{dt}}_{-\frac{Q(t)}{\tau_\text{rec}}} - \underbrace{\frac{\partial Q}{\partial V}}_{C(V)} \frac{d V(t)}{d t},$

where the first term on the right hand side represents the recombination rate – of which we want to measure the recombination lifetime $\tau_\text{rec}$ – and the second term a contribution coming from the response of charge due to the measured signal of the experimental technique: the time variation of the voltage as response to a time dependent light signal (pulsed or modulated). If the latter capacitive term becomes dominant, the recombination lifetime cannot be determined anymore, as is hidden behind the RC time.

As you can see in this slide, based on our data, for P3HT:PCBM (bottom left of the slide) the capacitive (RC) times remain lower than the measured time constants. We can state with some confidence that the RC times do not limit the measured recombination lifetimes. Also, the slopes of $\tau$ vs $V_{oc}$ are different and, in this case, a measure of the recombination order.

In contrast, for the PCDTBT:PC70BM solar cell, for which I took the measured time constants at room temperature from literature, you see that the RC time limits the recombination lifetime, as the measured time constants just correspond to the RC times. This implies that the recombination lifetime is too short to be measured for the given RC limitation.

A nice aspect of the paper by Kiermasch et al. is that it gives a comparatively simple way to estimate the RC times:

$\tau_{RC} \approx \frac{C(V_{oc})}{j_\text{gen}(V_{oc})} \frac{nkT}{e}$

Here, $nkT/e$ is the recombination ideality factor times the thermal voltage, $C$ is the voltage dependent capacitance, which can be estimated (as lower bound) by the geometric capacitance of the active layer, $C_\text{geo} = \epsilon_r\epsilon_0/L$ , with the dielectric constants (relative and vacuum) and $L$ the active layer thickness (you could also include organic transport layers, but probably not PEDOT:PSS as it has a relative dielectric constant $\gg$ 3). The generation current density can be approximated, in most cases, by the short circuit current density $j_{sc}$ (unless the transport resistance loss is too large:).

Please note, that in this particular RC time where both $R$ and $C$ come from the solar cell itself, the active area cancels out (as both $j$ and $C$ contain it and are in denominator and numerator, respectively). So, in order to reduce the RC time for a given solar cell, the only way seems to either 1. increase the current, by increasing the light intensity, measuring up to higher Voc… if possible, or 2. reduce the (geometric) capacitance by increasing the device thickness… a lot.

All of this came to my mind again when looking at IMVS data that we took on PM6:Y12 solar cell devices (made by Chen, measured by Nino with support from Christopher).
PM6-Y12 IMVS RC time vs IMVS time constant.
On the left, you see the estimation of the RC time $\tau_{RC}$ after Kiermasch 2018, compared to the measured time constants by IMVS, $\tau_c$ . Except for, maybe, low temperatures, the RC times dominate the measured signal at high open circuit voltages, whereas the shunt limits the lifetime determination at lower open $V_{oc}$ . A direct comparison is shown on the right hand side, where everything in the shaded triangle is either shunt or RC-limited.

While quite sad, I think this is important: if you want to determine recombination lifetimes in thin film solar cell devices, check for limitations by RC times and shunt.

Nongeminate recombination in organic solar cells – slower than expected

In a “recent” post (just 3 posts but 10 months ago;-) I wrote once again on the derivation of the Langevin recombination rate for nongeminate recombination. The question is, is Langevin recombination really what governs the charge carrier loss rate in organic solar cells?

Recombination of electrons with holes is usually a 2nd order decay. As electrons $n$ and holes $p$ are photogenerated pair wise, the respective excess charge carrier concentrations are symmetric, $n=p$ . Then a recombination rate $R$ is

$R = k n p = k n^2$ ,

where the recombination prefactor $k$ could be a Langevin prefactor – more on that later. In a transient experiment with a photogenerating, short laser pulse at $t=0$ , the continuity equation for charge carriers (here, e.g. electrons) under open circuti conditions (no external current flow, for instance if the experiment is done on a thin film without electrodes)

$\frac{dn}{dt} = G-R$

becomes

$\frac{dn}{dt} = -R$

for $t>0$ (as the generation was only at $t=0$ ).

If all electrons and hole are available for recombination (i.e., can reach all other charge carriers and can be reached by them), then the recombination rate and the continuity equation for $t>0$ yield

$\frac{dn}{dt} = k n^2$ Continue reading “Nongeminate recombination in organic solar cells – slower than expected”

Nongeminate Recombination: Langevin (again) and beyond (later;-)

Nongeminate recombination is the major loss mechanism for state-of-the-art organic solar cells. In an early blog post, I showed how the Langevin recombination was derived.

Although there is more to nongeminate recombination than just this mechanism, it is still instructive and also relevant to trap-assisted recombination mechanisms, due to its mobility-containing prefactor.

[Nenashev 2010] pointed out that in the derivation of the Langevin recombination,

since the electric field scales as r⁻² and the surface area of the sphere scales as ², the value of r chosen is unimportant, leading to a simple solution with constant electron den- sity, thus justifying the neglect of diffusion.

Continue reading “Nongeminate Recombination: Langevin (again) and beyond (later;-)”

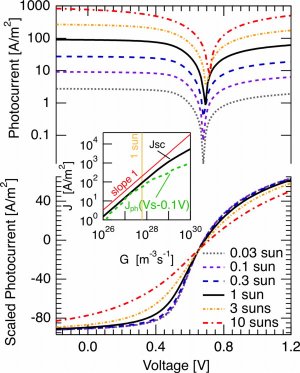
Photocurrent in organic solar cells – Part 2 [Update]

Almost a year ago, I already discussed the photocurrent in organic bulk heterojunction solar cells. Also, recently I posted about the difficulties to determine the dominant loss mechanism from the short circuit current density dependence on the light intensity. Today, I would like to extend these statements to the photocurrent in somewhat more general terms.

The figure to the right contains the simulated photocurrent for a bulk heterojunction solar cell of 100nm thickness at room temperature. Parameters were chosen according to typical experimentally determined values for P3HT:PCBM solar cells: Bimolecular Langevin recombination with a reduction factor of 0.1 and electron and hole mobility of 10^-4m²/Vs were assumed (is it possible I never discussed this reduction really? Seems so, just mentioned it with references here). The top graph shows the photocurrent, in the lower graph the photocurrent was divided by the illumination density in terms of suns (thus, the current densities given on the y-axis are only correct for 1 sun). Consequently, if the photocurrent scales linearly with the light intensity, all curves should coincide. Let me remind you that this was interpreted by different groups (Street et al. among them, but not the first to follow this explanation) as a sign of first order recombination.
Continue reading “Photocurrent in organic solar cells – Part 2 [Update]”

From Newton to Hawking

Via c’t: as the British Royal Society turns 350, several historical works are available online for the first time. Not only physics, but also medicine etc… In the nice timeline, you find Newton’s theory of light and colour in the year 1672. It links to Phil. Trans. 1 January 1671 vol. 6 no. 69-80 3075-3087. Quite amazing!

Add to Connotea

Influence of Finite Surface Recombination Velocity on Efficiency vs. Mobility of Polymer Solar Cells

Just a quick addition to Mobility and Efficiency of Polymer Solar Cells. You might remember that with increasing mobility, the

open circuit voltage Voc, however, decreases steadily. Actually, the slope steepness is maximum due to our implicit assumption of ideal charge extraction ; for a realistic charge extraction (= finite surface recombination), the Voc slope with mobility is weaker… or even constant for zero surface recombination. The fill factor is maximum at intermediate charge carrier mobilities, not far from the experimentally found values!

As we were finally able to calculate the open circuit voltage with a surface recombination less than infinity (thanks to Alexander Wagenpfahl),
I can show you how it looks. ([Update 3rd March 2010] For details, have a look here: [Wagenpfahl 2010, arxiv]) Continue reading “Influence of Finite Surface Recombination Velocity on Efficiency vs. Mobility of Polymer Solar Cells”

Photocurrent in organic solar cells – Part 1

In at least two previous posts (Picture Story and How do organic solar cells function – Part 1), I highlighted the field dependence of the photocurrent in organic solar cells, and its connection to the polaron pair dissociation. Actually, there is more to it.

The field dependence of the photocurrent is due to different contributions:

polaron pair dissociation (bulk heterojunctions and bilayers)
polaron recombination (mostly bulk heterojunctions)
charge extraction (bulk heterojunctions and bilayers)

An experimental curve of the photocurrent of a P3HT:PCBM solar cell is shown in the figure (relative to the point of optimum symmetry, as described by [Ooi 2008]. The symbols show our experimental data, the green curve a fit with two of the contributions mentioned above: polaron pair dissociation (after [Braun 1984]) and charge extraction (after [Sokel 1982]). Both models are simplified, but more on that later. 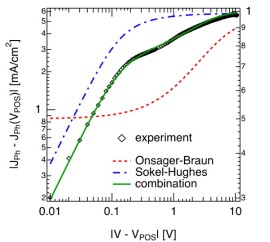Polaron recombination has been covered before (here and here); it is pretty low in state-of-the-art bulk heterojunction solar cells, and has therefore been neglected. For now, lets concentrate on the contribution from polaron pair dissociation. For the sample shown in the figure, the separation yield approaches 60% at short circuit current (at about 0.6V on the rescaled voltage axis, 0V corresponding to the flatband case). The question is, why is it so high in polymer-fullerene solar cells, considering that a charge pair has a binding energy og almost half an electron Volt at 1 nm distance, and that recombination is on the order of nanoseconds [Veldman 2008].

Continue reading “Photocurrent in organic solar cells – Part 1”

Mobility and Efficiency of Polymer Solar Cells

Disordered organic materials inhibit charge carrier mobilities which are orders of magnitude lower than for inorganic crystals. First thing missing in disordered matter is the regularly ordered lattice of atoms, where the charge carriers can delocalise, leading to band transport. Second thing is the generally lower interaction between adjacent molecules, which is due to weaker bonding and larger distances. The transfer integral, the value of which goes exponentially down with distance, to get from one to the other molecule is too low for delocalisation. Thus, in terms of charge carrier mobility, think 10^-2cm²/Vs for disordered organics (if you are lucky) vs. at least 10²cm²/Vs for ordered inorganics.

How much does a weak charge transport limit the performance of organic solar cells? How bad is it?

Continue reading “Mobility and Efficiency of Polymer Solar Cells”

Trimolecular Recombination … really?

As you might already have guessed, I am interested in loss mechanisms in organic photovoltaics. Despite considering the impact of recombination on the solar cell performance, also the physical origins are challenging… and many open questions remain.

Just a view days ago, there was another publication about recombination of free polarons (free carriers) – also called nongeminate recombination *¹ – more specifically, trimolecular recombination. You might remember that, a while ago, I already mentioned third order recombination, including a reference to private communications with Prof. Juska and another recent paper by the Durrant group [Shuttle 2008]) as well as a potential candidate for its origin. The new paper [Juska 2008] uses three different experimental methods, including photo-CELIV, to measure the temperature dependence of the trimolecular recombination rate in polymer:fullerene solar cell. The authors mention very briefly a possible mechanism responsible for the third order recombination, Auger processes. Shuttle et al. argue in their paper that a bimolecular recombination with a carrier concentration dependent prefactor could be the origin, in particular as they observe a decay law proportional to n^2.5-n^3.5, depending on the sample. We are also in the game, an accepted APL awaiting its publication (preprint here) Update 20.10.2008: now published online [Deibel 2008b]. We rather tend to believe the explanation by Shuttle, but that’s just an assumption at the present stage: the generally low recombination rate could also be due to a rather improbable process.

Continue reading “Trimolecular Recombination … really?”

	Transport resistance… on The transport resistance in or…
	Pitfalls when measur… on The transport resistance in or…
	deibel on The transport resistance in or…
	deibel on The transport resistance in or…
	Julien Gorenflot on The transport resistance in or…
	Julien Gorenflot on The transport resistance in or…
	deibel on The transport resistance in or…
	deibel on The transport resistance in or…
	Julien Gorenflot on The transport resistance in or…
	Julien Gorenflot on The transport resistance in or…