The transport resistance in organic solar cells

In one of my last posts on the diode ideality factor (6 years ago…), I promised to talk about the transport resistance in organic solar cells. Cornudella de MontsantI came across it already during my time at IMEC in Leuven, Belgium, around 2004: my colleagues and I worked on an analytic model of the open circuit voltage in organic bilayer solar cells. The corresponding paper was published a few years later, [Cheyns et al 2008], but I have to admit that I did not grasp its importance as a relevant loss mechanism for organic solar cells in general, focussing on geminate and nongeminate recombination – until this paper by [Würfel/Neher et al 2015] came out. I think now I have;)

The transport resistance is an internal resistance in the active layer (or transport layer(s)) of the solar cell, acting like an internal series resistance: It changes the slope of the current density–voltage characteristics – for instance around the open circuit voltage – and thus reduces the fill factor.

If you can live with an effective conductivity \sigma_\text{eff} = e n_\text{eff} \mu_\text{eff} for now, I’d say that the transport resistance is given as

R_{tr}= \frac{1}{e} \int_0^L \frac{1}{n_\text{eff}(x) \mu_\text{eff}(x)} \text{d}x \approx \frac{L}{\sigma_\text{eff}}

with the effective carrier concentration n_\text{eff}, the effective mobility \mu_\text{eff}, and the active layer thickness L. For a finite current j, the externally applied voltage V_\text{ext} of the j(V_\text{ext}) curve (red in the sketch) 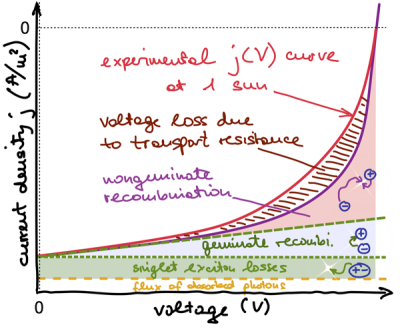losses in current-voltage characteristics is reduced by \Delta V = V_\text{ext} - V_\text{int} =j R_{tr} as compared to the transport resistance free case which I call j(V_\text{int}) (violet). The reason is that the electron and hole energy levels equivalent to conduction and valence band are more tilted due to the influence of the low conductivity. Rod MacKenzie from Durham used his drift–diffusion simulation programme gpvdm – which among many other features allows to use the multiple-trapping-and-release model to account for energetic disorder – to calculate an example. In the figure, the energy levels corresponding to conduction and valence band are shown, and the yellow shading between the band edges correspond to the trap populations which I will ignore. So focus on the edges! 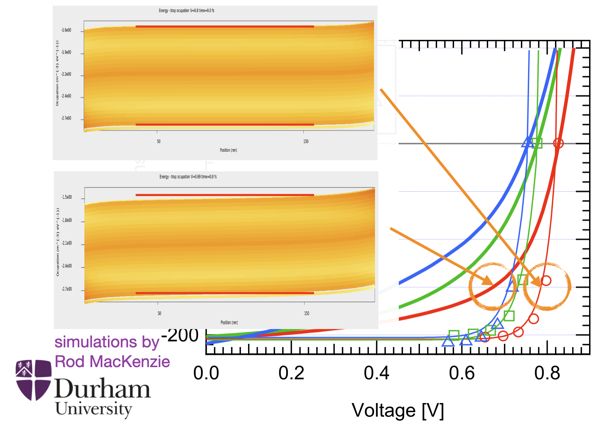Band bending due to transport resistance, by Rod MacKenzie using gpvdm The upper left inset features the band bending of the transport resistance free case at a current–voltage point in the fourth quadrant of an illuminated solar cell, V_\text{int} being at 0.8 V. The red lines show that in the bulk, the bands are perfectly flat despite not being at any “flat band” voltage. In contrast, the lower left inset shows the band bending for the illuminated current–voltage point at the same current, but at V_\text{ext} of 0.69 V. The voltage difference \Delta V of 0.11 V is due to the transport resistance. The two perfectly horizontal red lines, just shifted down from above, now show a discrepancy due to the band bending in the bulk. This tilt sums up to the voltage loss \Delta V, and corresponds to a gradient of the quasi-Fermi levels, as discussed clearly in [Würfel/Neher et al 2015] around Eqn (8). Let me note that the denomination of V_\text{int} as opposed to V_\text{ext} is a bit unfair, as the latter still drops across the whole (active) layer thickness L – but the gradient is different. So, can the two different band bendings (upper left and upper right) occur at the same time? No of course not. The lower right shows you how a simulated organic solar cell with realistic parameters looks inside: it is limited by a transport resistance due to low effective conductivity in the active layer, which shows up as tilt in the bands, and implies a gradient in the quasi-Fermi levels. The upper right shows you how the bands looked if the solar cell were not limited by a transport resistance (and how they do look under the special case of open circuit conditions).

Still, the voltage drop due to the transport resistance – coming from the low conductivity and leading to the tilted transport levels – is real and does reduce the fill factor.

In my recent talk at the MRS Spring meeting (invited! in person! on Hawaii! slides here:), I showed the approximate difference of the internal and external voltage of a fresh, inverted PM6:Y6 bulk heterojunction solar cell (L = 200 nm, but qualitatively similar for 100 nm) at different light intensities, from 3 micro-suns to 1 sun (300 nW/cm2 to 100 mW/cm2). Sa Vint vs Vext The ideal diagonal case where V_\text{int}=V_\text{ext} is only seen for the lowest light intensities. In contrast, at 1 sun illumination, when 0.4 V are applied, the internal voltage is still at around 0.7 V. The fill factor at 1 sun is, by the way, somewhat above 60%, whereas the transport resistance free pseudo fill factor (determined using the Suns-Voc method, see below) is above 80%. As If you are interested in the details of this study, please have a look at our preprint. [Update 2022-07-01]: now published in Nature Communications.

How did we determine the approximate internal voltage, or j(V_\text{int}), when we only have direct access to the external (i.e., applied) voltage? Similar to [Schiefer et al 2014], we used the Suns-Voc method as a measure for the series and transport resistance free current–voltage characteristics. The idea is in the post on the diode ideality factor, but before sending you away again I repeat it here: the current density, as given by the diode equation under assumption of the superposition principle,

j = j_0 \left( \exp\left(\frac{q(V_\text{ext}-jR_s)}{nkT} \right) -1 \right) - \frac{V_\text{ext}-jR_s}{R_p} - j_\text{gen} (*)

is influenced by the series resistance R_s and parallel resistance R_p. At open circuit, V_\text{ext} = V_\text{int} = V_{oc}, the current j(V_{oc}) is zero,

0 = j_0 \left( \exp\left(\frac{q(V_{oc}-0 R_s)}{nkT} \right) -1 \right) - \frac{V_{oc}- 0 R_s}{R_p} - j_\text{gen},

so that the terms including the series resistance (but not the parallel resistance!) become zero as well. Reordering the equation,

j_\text{gen} = j_0 \left( \exp\left(\frac{qV_{oc}}{nkT} \right) -1 \right) - \frac{V_{oc}}{R_p},

we have an equation very similar to the diode equation (*). The pairs j_\text{gen}(V_{oc}) measured under a wide range of light intensities can, when shifted down by j_{sc}(\text{1 sun}), correspond to the so called Suns-Voc curve. It represents the j(V_\text{int}) curve, as the open circuit voltage is transport resistance free so that (only) there, \Delta V=0. The Suns-Voc curve is equivalent to the illuminated j(V_\text{ext}) curve, but lacks the influence of the series and transport resistance. The generation current j_\text{gen} \approx eGL with the generation rate G is sometimes (ok, often..) approximated by the short circuit current j_{sc}.
An example of how a Suns-Voc curve looks is shown in my earlier post on the diode ideality factor in the third figure (red = illuminated j(V_\text{ext}), green symbols = Suns-Voc curve).

Of course there is a better way by measuring both the voltage dependent current and luminescence of a solar cell, as done by [Rau et al 2020] on Cu(In,Ga)Se2 solar cells: from the luminescence, which depends on the quasi-Fermi level splitting, the internal voltage can be determined. For organic solar cells, as singlet and charge transfer exciton photoluminescence need to be separated – the internal voltage will be proportional to the latter – this is harder and has not been done yet, as far as I know.

How can the impact of the transport resistance on the fill factor, and thus performance, of organic solar cells be minimised? To reduce the transport resistance, the active layer conductivity needs to be increased. This can be done by, either, increasing the charge carrier mobility – for a molecular hopping system this means reducing static (low \sigma) and/or dynamic disorder (low \lambda). Or, increasing the carrier concentration – e.g. by doping, which is kind of hard in a bulk heterojunction, but starting with the material phase with the lower conductivity could be a viable approach.

Some hat tips here beyond the very nice cooperation of our study: Maria and Rod for feedback to an earlier version of the post, and Julien for being the first commenter on it:)

8 thoughts on “The transport resistance in organic solar cells”

  1. Hallo! So nice to see your blog a life again! So let’s make it live even more with a question: do you think large ideality factor and large transport resistances are 2 consequences of the same problem (traps), or 2 different effects? or maybe there’s not enough elements yet to answer? but I guess the simulations you mention must have the answer.

    Reply

    1. Thanks, Julien!

      I reckon it makes sense to distinguish the diode ideality factor due to recombination (I call it also recombination ideality factor), which is seen in both illuminated j(V) curve and Suns-Voc curve, and the impact of the transport resistance on the illuminated j(V) curve (or the dark one!). For the recombination ideality factor, it makes sense in any case to determine it from the Suns-Voc (which is a light-intensity dependent Voc) measurement. This is for instance explained in [Tvingstedt/Deibel 2016]). The effect that the transport resistance has on the “apparent” ideality factor of the illuminated j(V) curve – the latter including the recombination ideality factor as well as the impact of the transport resistance – was described in some detail by [Neher et al 2016]: they introduced the figure of merit α, which is essentially an approximation for the impact of the transport resistance on the apparent ideality factor – with the simplification that the recombination ideality factor is fixed to unity in their approximation. In short, then, the apparent ideality factor around Voc comes out as 1 + α.

      To come to your question, a recombination ideality factor exceeding unity (not necessarily “large”, but still;) is usually a result of 1. trap-assisted recombination, and 2. – in organic solar cells being energetically disordered with hopping charge transport – not all charge carriers being available for recombination (as trapped electrons and trapped holes cannot meet one another, which I believe I never spelled out explicitly in this blog, only implicitly; see e.g. [Göhler et al 2018, pg 7]). In particular the second point implies that more trapping leads to higher ideality factor, with values beyond two becoming possible (especially at lower temperatures where the effective disorder, the actual energetic disorder relativ to the thermal energy, is higher). A contribution of a high transport to the “apparent” ideality factor (leading, in the Neher framework, to a high value of α), is due to a low conductivity: a reason for this can also be trapping. How trapping influences the recombination ideality factor and the impact of the transport resistance on the “apparent” ideality factor will not be necessarily similar, though. If an exemplary organic solar cell were governed by the classical Langevin recombination, for instance (where the recombination rate is given by the sum of electron and hole mobility), lower electron and hole mobilities would reduce both recombination rate and extraction rate – which could in the simplest case lead to the same fill factor as before because recombination/extraction rate would not change – but the transport resistance would be higher and reduce the fill factor… but not the pseudo fill factor.

      I will stop here for now, but I am happy to dig deeper if useful:)

      Reply

      1. Thanks for the answer, I recall there used to be a plan for a full post on this :p

        “So, what’s next. I plan to write two more posts on the ideality factor, one on its relation to the recombination rate, and one the transport resistance (see recent papers by [Würfel/Neher et al 2015] and [Neher/Koster et al 2016].”

        Now that you have defined the 3 variables separately, the stage is ready :)
        But thanks for this introduction to it already. I think the detailed and illustrated post would still be totally worth interesting :)

      2. Thank you:) Indeed I want to follow up, but a large project defense is coming up end of September and I do not have the nerve to write blog posts just now. Will come though, reminder welcome;)

      3. btw I also wanted to bounce back on this, as that’s something I’ve been wondering for a few months…

        “for instance (where the recombination rate is given by the sum of electron and hole mobility), lower electron and hole mobilities would reduce both recombination rate and extraction rate – which could in the simplest case lead to the same fill factor as before because recombination/extraction rate would not change –”

        I have exactly this problem in many papers of my students or colleagues. They show high or low recombination rates, but I always want to reply “so what?” I mean, you can have good cells with a lot of recombination if the extraction is even faster.

        Do you have a metric in mind to really compare recombination with extraction? For the reason you just mentioned, the reduction factor to Langevin recombination rate kind of does that, but it’s somewhat by chance :p

        Well…. of course by chance or not, it’s better than nothing I guess. Well, maybe J/Jsat kind of does that too but it includes too many other effects…

      4. Well, I think the classical metric to compare the extraction-vs-recombination is the lifetime–mobility product (\mu \tau), which directly impacts the fill factor. The lifetime usually does, of course, depend on the carrier concentration, and actually both electron and hole mobility might go differently into transport and recombination (in the latter e.g. as geometric mean of mobilities), so this is hard to do analytically. Recombination alone would, of course, influence the open circuit voltage in addition, so minimising recombination has its separate merits. The same goes for the mobility / conductivity, as increasing it will descrease the transport resistance.

        The figures of merit for instance introduced in the linked 2016 SciRep paper of Dieter Neher with Jan Anton Koster is already what is needed to see the effect of mobility vs recombination on the fill factor, just that effect of recombination and transport resistance are not distinguished. We meant to do this but have not gotten to it;-)

Leave a comment