Nongeminate recombination in organic solar cells – slower than expected

In a “recent” post (just 3 posts but 10 months ago;-) I wrote once again on the derivation of the Langevin recombination rate for nongeminate recombination. Tiger (Zoo Wuppertal)The question is, is Langevin recombination really what governs the charge carrier loss rate in organic solar cells?

Recombination of electrons with holes is usually a 2nd order decay. As electrons n and holes p are photogenerated pair wise, the respective excess charge carrier concentrations are symmetric, n=p. Then a recombination rate R is

R = k n p = k n^2,

where the recombination prefactor k could be a Langevin prefactor – more on that later. In a transient experiment with a photogenerating, short laser pulse at t=0, the continuity equation for charge carriers (here, e.g. electrons) under open circuti conditions (no external current flow, for instance if the experiment is done on a thin film without electrodes)

\frac{dn}{dt} = G-R

becomes

\frac{dn}{dt} = -R

for t>0 (as the generation was only at t=0).

If all electrons and hole are available for recombination (i.e., can reach all other charge carriers and can be reached by them), then the recombination rate and the continuity equation for t>0 yield

\frac{dn}{dt} = k n^2which can be solved analytically:

n(t) = \frac{n(0)}{1 + k n(0) t} \propto t^{-1}.

That means, on a log-log n(t) plot (or \Delta OD(t) for a transient absorption experiment), the transient due to charge carrier recombination in a second order decay has a slope of -1.

It is no news that slower decays

n(t) \propto t^{-\frac{1}{\delta-1}}

with higher recombination order \delta>2 are reported in literature by transient absorption experiments [Montanari 2002, Offermans 2003] and recently also using other techniques, see references in this post. This corresponds to recombination rates of the empirical form

R \propto n^\delta.

Clearly, this is not a second order recombination. However, it is very unlikely that more than two charge carriers are involved (c.f. this post). Thus, can it actually be Langevin recombination?

[Shuttle 2010] proposed that this could still be Langevin recombination, where the order of decay higher than originates from the charge carrier mobility. That implies that all charge carriers can recombine with one another, but the charge carrier mobility in the Langevin prefactor depends on the charge carrier concentration. The latter is credible, as the macroscopic mobility in a system with a lot of charge carrier trapping (and there is! [Schafferhans 2010]) can indeed depent on the carrier concentration [Tanase 2003, Pasveer 2005] – depending on the density of states distribution [Oelerich 2012]. Then,

R \propto \mu(n) n^2 \propto n^{\text{something }>0} n^2 \propto n^\delta.

That was easy;)

But is it the complete explanation? That may not be the case. We showed last year [Rauh 2012], that often

\frac{R}{n^2} \not\propto \mu(n),

opposing the above statement (1). However, a weakness of both studies is that the mobility is not measured directly – still to be done.

In the meantime, a very interesting paper [Kirchartz 2011] (you need to take some time for it, though;-) – and slightly later also [Kuik 2011] – showed that Langevin recombination and trapping should be combined in a more detailed way. If you consider that some charge carriers, say electrons, in the disordered organic semiconductor are mobile, with density n_c, and some are trapped, n_t, their sum still equals the overall electron concentration $n$. As long as the charge carriers n_t remain trapped, they are immobile and cannot move towards their recombination partners. That means, they cannot actively contribute to recombination, but can be “found” by another (oppositely charged) charge carriers. The recombination rate for recombination of a mobile electron with a trapped hole can be written as

R \propto \mu_e n_c p_t

or, if electron and hole concentrations as well as their trap distributions are assumed to be the same,

R \propto \mu_c n_c n_t.

Importantly, the mobility \mu_c is not the measured macroscopic mobility, but the maximum possible mobility without trapping.

With two assumptions, this equation can be brought into the Langevin recombination shape again: (1) the concentration of trapped carriers by far exceeds the mobile ones (which makes sensse as charge carrriers tend to relax down in energy), n_c \ll n_t, so that $n_t \approx n$, and (2) the mobility and the actual recombination process are governed by the same density of (trap) states distribution. Then, from the multiple-trapping-and-release model, which I’ll hopefully write more on another time, the macroscopic mobility \mu(n) is connected to the high local mobility \mu_c by \Theta = \mu(n)/\mu_c, and at the same time the so-called trapping factor \Theta=n_c/n! Therefore, the last equation can be written as

R \propto \mu_c n_c n_t \approx \mu_c n_c n = \mu(n) n^2.

Thus, in principle the nongeminate recombination of charge carriers in organic solar cells, even with trapping, Recombination free trapped only after emission
could be described by the Langevin recombination rate. Under these conditions, it is very similar to Shockley-Read-Hall recombination (in contrast to what I wrote in a comment a few years back!).

However, the discrepancy (1) mentioned above, \frac{R}{n^2} \not\propto \mu(n), still remains and needs to be resolved. While I believe that Langevin recombination can also in the future be used to describe nongeminate losses in organic solar cells, I think it will have to be further adapted (i.e., also the last equation) – for instance in view of probably partial phase separation, where not every mobile charge carrier can actually meet a trapped one, if the latter is deep within one material phase [Baumann 2011].

6 thoughts on “Nongeminate recombination in organic solar cells – slower than expected”

  1. Hi Carsten,

    Nice post. I have some transient absorption evidence for simple second order recombination of charge carriers in P3HT:PCBM in my Ph.D thesis. Won’t you have a look?

    In general I came to similar conclusions to some of the above authors but with a different outlook on the Langevin prefactor constant to you;

    Taking some of the above statements as ‘true’;

    “As long as the charge carriers remain trapped, they are immobile and cannot move towards their recombination partners. That means, they cannot actively contribute to recombination.”

    and

    “for instance in view of probably partial phase separation, where not every mobile charge carrier can actually meet a trapped one, if the latter is deep within one material phase”

    These mean that a trapped charge can not recombine! The type of recombination observed depends then on the charge carrier concentration and the number of traps.

    For charge densities above the trap densities (hence traps are filled), the recombination should appear second order

    for densities below the trap density you see delayed recombination due to de-trapping times being recombination rate limited.

    So far no problem. But then taking this further;

    The Langevin pre-factor that comes out of the second order decays should be interpreted as either a measure of the available surface area at the interface between donor and acceptor phases or as a measure of average mobility of the charges, depending on which is rate limiting. The logic behind this is that recombination can only take place at the interface.

    For instance, where mobilities are slow but recombination at the interface is fast, charges moving from the bulk of the donor or acceptor phase have to migrate to the interface before they can recombine. Recombination is fast compared to mobility and so mobility is the only thing that counts towards controlling the rate, giving you the typical Langevin outlook on recombination.

    Where you have high mobilities and charges from the deep bulk of the donor acceptor phases move in and out of the interfacial area many times before recombining with a partner opposite charge then the Langevin prefactor does not have anything to do with mobility and only with the surface area. This is a break from the traditional idea of Langevin on the prefactor but is logical if you consider that Langevin was for single layer materials only. The recombination is still second order because your bulk concentration controls your surface ( or interface) recombination but the prefactor is a reflection of the effectiveness of the recombination at the interface. The prefactor then could tell you something about the nature of the interface.

    To my mind mobilities for mobile charges in solar cells are high (if not that wouldn’t be good for current!) so the prefactor tells us most about the surface area for recombination. This was backed up by preliminary findings suggesting that annealing had a negative effect on recombination rates despite the increased expected charge mobilities.

    So for me no calculations involving mobilities needed!

    Reply

    1. Thanks for your input. I’d link to your thesis, but that would tell people who you really are… We also performed TA measurements etc, and as I write below we do not see only 2nd order decay for P3HT:PCBM and other materials. Also, I can agree only with the smaller fraction of what you write, but in a discussion that is all the more enjoyable;-)

      “These mean that a trapped charge can not recombine!” – That is correct only for perfect phase separation, which is certainly not the case, therefore I spoke about partial phase separation. I’ll briefly come back to that case below, see (*).

      “For charge densities above the trap densities (hence traps are filled), the recombination should appear second order” – that is true, but keep in mind that photogenerated mobile charge carriers due relax with time. For PTB7:PC70BM thin films, one nicely sees first 2nd order decay, then trap assisted recombination once relaxation is finished. For P3HT:PCBM, recombination is directly trap assisted, i.e. higher order recombination. Similar to you, we also performed TA measurements on these systems, and for P3HT:PCBM we see *almost* 2nd order decay at room temperature, but always a bit more, using either of transient absorption, OTRACE or transient photovoltage/charge extraction. At lower temperatures we see higher recombination orders, which can neither be explained by simple Langevin recombination nor by the available surface.

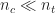      “Mobilities are slow” – actually, for a system without perfect phase separation, you will get 2nd order decay only before charge carrier relaxation: then, n_c \approx n_t, whereas after relaxation n_c \ll n_t. The only other case where you will see 2nd order decay (for a range of temperatures, not just 300K!) is in a homogeneous system without (donor-acceptor) phase separation, such as neat P3HT!

      “High mobilities” – well, they are only high before relaxation or on a local scale. You state that the available surface area will govern the recombination. I agree that it will have *some* impact, but I disagree with your conclusions. The recombination is *not* second order, in particular at lower temperatures the order of decay is higher. The recombination rate is something with n_c n_t, possibly with a constant prefactor <1 which accounts for the geometrical impact of the surface area. (*) If, in contrast, the recombination order were still 2, then trapped charge carriers would not be able to recombine (before re-emission), and the recombination rate were n_c^2. However, (1) even that the prefactor would include the mobility, and (2) I have never yet seen that case.

      Reply

  2. I want to register in PhD but I’m lost in the choice of subject could you help me? I want to know what are the latest research on organic photovoltaics?

    Reply

  3. or for exemple what are the main issue concerning monocomponent BHJ devices using self-assembled D-A semiconductor liquid crystals

    Reply

  4. Hi Carsten,
    Thanks a lot for the post.
    A Langevin-type recombination (= transport-limited recombination) means that a hole recombines upon its first close encounter with an electron. consider a system in this regime of recombination. Do the injected carriers into the system have enough time for thermal relaxation before the recombination?
    In a reaction-limited recombination, since the recombination time scale is much larger than the transport one, the carriers have time for relaxation before a recombination event occurs.
    —-
    the link [Kirchartz 2011], in the middle of the post, doesn’t work.

    Reply

    1. Hi, good question. In a reaction-limited system – i.e. with high mobility, implying a high degree of order or band transport – I would not expect that the carriers *need* to relax. On the other hand, in thin films I would expect that charge carriers can be unrelaxed – if they are optically excited. (As injection is (in the easiest case) according to thermal emission, I would expect that the injected charge carrier package is already on average lower in energy than an optically excited one.) If they really are unrelaxed depends on temperature, disorder etc.. For encounter limited transport the distance to the recombination partner is less than the distance to the electrode, therefore a recombining charge carrier may be less relaxed than an extracted one. Cheers, also for notifying me of the broken link – I fixed it.

      Reply

Leave a comment