Tag: transport resistance

Transport resistance strikes back

Since the last time that I wrote on transport resistance as a voltage loss mechanism in organic solar cells, due to low active layer conductivities, we have continued working on it. double rainbow seen from the institute of physics in Chemnitz
While we learnt from our valued colleague Prof. Chang-Qi Ma that MoOx diffusion contributes strongly to fill factor losses by thermal degradation – they had published their convincing results in [Qin 2023], under our radar – we also understand better how to recognise and comprehend transport resistance losses.

The simplest way to characterise transport resistance is to determine the difference between a normal current density–voltage curve under 1 sun, and the suns-Voc curve. The latter is the pair-wise combination of generation current density and open-circuit voltage that is giving one current density-voltage point per light intensity: doing this for a wide range of light-intensities results in a pseudo-JV curve. To compare this suns-Voc curve to the current density–voltage curve under 1 sun, it has to downshifted so that the open-circuit voltage of both curves coincide on one point: j(V) = (0, V_{oc}). The result could look like the scheme shown in the figure below. I have adapted this figure from Maria’s new publication on transport resistance losses in organic solar cells [Saladina 2025] (the title is Transport resistance strikes back: unveiling its impact on fill factor losses in organic solar cells ;-). The j(V_\mathrm{external}) curve (blue) is the normal JV curve under illumination, where V_\mathrm{external} is the applied voltage. The down-shifted suns-Voc curve corresponds to the j(V_\mathrm{implied}) (red); the implied voltage is the voltage without any series-resistance imposed drops. In other words, the externally applied voltage drops over the diode and all series resistances, the external series resistance as well as the transport resistance that comes from a low active layer (or transport layer) conductivity. The implied voltage, as measured by the open-circuit voltage (at zero current, where series resistances do not play a role), corresponds to the voltage without drops over series and transport resistance. 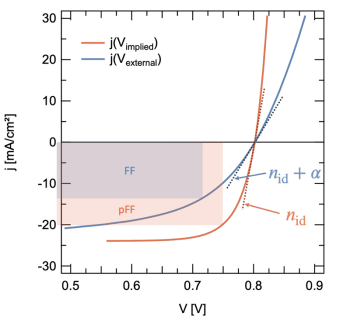If a solar cell has a low active layer conductivity and is transport resistance limited, than the measurement of the suns-Voc curve to construct the j(V_\mathrm{implied})-curve allows to evaluate the performance of that solar cell as if it did not have any transport resistance losses. One could also say: while the measured j(V_\mathrm{external}) curve is transport resistance limited, the pseudo-j(V_\mathrm{implied}) curve corresponds to the case of infinite conductivity, but contains the same recombination as the measured curve.

Also indicated in the figure are two further figures-of-merit to distinguish the measured JV curve and the series resistance-free pseudo-JV curve: the slopes around the open circuit voltage (indicated in the figure by n_{id} and n_{id}+\alpha), and the fill factors – FF and the pseudo-FF. The FF is generally defined as fraction of the power at the maximum power point over the power given by short circuit current times open circuit voltage, j_{mpp} V_{mpp} / j_{sc} V_{oc}. The pseudo-FF does essentially the same, but for the series and transport resistance-free pseudo-jV curve. The normal FF (blueish) is not a measure of just recombination, but of recombination and series and transport resistance losses! The pseudo-FF (reddish) is due to only recombination losses. The difference between pFF and FF is, therefore, a measure of the transport resistance losses that the organic solar cell has.

The suns-Voc curve is used in the literature to determine the recombination ideality factor of solar cells. Even on the linear scale, the (inverse) slope of the corresponding j(V_\mathrm{implied})-curve around Voc is given by the ideality factor n_{id}. The j(V_\mathrm{external}) curve has a slope which is given by the ideality factor and a figure-of-merit describing the transport resistance: \alpha. It was introduced by [Neher 2016], and I state it here in its general form,
\alpha = \frac{eL}{kT} \frac{j_\mathrm{gen}}{\sigma_{oc}},
where the recombination current density equals j_\mathrm{gen} at V_{oc}, and \sigma_{oc} is the effective conductivity at open circuit. L is the active layer thickness, and kT/e the thermal voltage. That means, \alpha increases when the active layer conductivity decreases. Correspondingly, the slope of the jV curve under illumination (the j(V_\mathrm{external}) curve) becomes less steep and the FF goes down: these are the transport resistance losses.
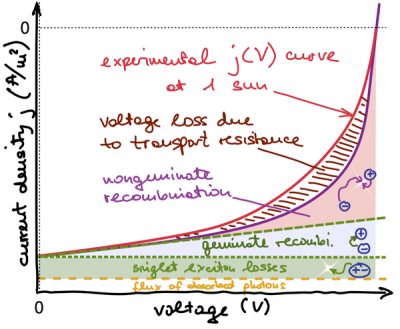
FF vs Voc due to transport resistance. For a selection of devices that we characterised for [Saladina 2025], we show on the right-hand-side the impact of transport resistance on the fill factor. The upper limit of the FF (solid line) can be reached when the recombination ideality is unity and there are no transport resistance losses. The FF (open circles) is often much lower, but in modern devices such as PM6:Y6 it can exceed 75%. The pseudo-FF (filled circle), however, is much closer to the upper limit, and is due to the trap-assisted recombination found in organic solar cells, at ideality factors that are often larger than unity. All in all, the largest loss for the fill factor is the transport resistance loss, essentially the difference between the pseudo-FF and the FF, even for the (not shown here) record-efficiency organic solar cell devices! I believe it makes a lot of sense to quantify the transport resistance in all publications that present the performance organic solar cells, so to avoid drawing wrong conclusions – for instance, that a given low fill factor is due to recombination, when the FF loss is likely dominated by low active layer conductivities. This is even more important when looking at the losses of organic solar cells with thicker active layers.

If you want to understand more about the transport resistance loss, I recommend (and self-advertise:) Maria’s paper, [Saladina 2025]. It contains information on how to predict the pseudo-FF just from the recombination ideality factor, how the conductivity of the active layer can be determined from the transport resistance, that \alpha is actually voltage dependent and not the best measure to describe the FF losses, how energetic disorder influences transport resistance, and how transport resistance losses can be minimised. As always, I am happy to hear your thoughts, in the comments or by email.

The transport resistance in organic solar cells

In one of my last posts on the diode ideality factor (6 years ago…), I promised to talk about the transport resistance in organic solar cells. Cornudella de MontsantI came across it already during my time at IMEC in Leuven, Belgium, around 2004: my colleagues and I worked on an analytic model of the open circuit voltage in organic bilayer solar cells. The corresponding paper was published a few years later, [Cheyns et al 2008], but I have to admit that I did not grasp its importance as a relevant loss mechanism for organic solar cells in general, focussing on geminate and nongeminate recombination – until this paper by [Würfel/Neher et al 2015] came out. I think now I have;)

The transport resistance is an internal resistance in the active layer (or transport layer(s)) of the solar cell, acting like an internal series resistance: It changes the slope of the current density–voltage characteristics – for instance around the open circuit voltage – and thus reduces the fill factor.

If you can live with an effective conductivity \sigma_\text{eff} = e n_\text{eff} \mu_\text{eff} for now, I’d say that the transport resistance is given as

R_{tr}= \frac{1}{e} \int_0^L \frac{1}{n_\text{eff}(x) \mu_\text{eff}(x)} \text{d}x \approx \frac{L}{\sigma_\text{eff}}

with the effective carrier concentration n_\text{eff}, the effective mobility \mu_\text{eff}, and the active layer thickness L. For a finite current j, the externally applied voltage V_\text{ext} of the j(V_\text{ext}) curve (red in the sketch) losses in current-voltage characteristics is reduced by \Delta V = V_\text{ext} - V_\text{int} =j R_{tr} as compared to the transport resistance free case which I call j(V_\text{int}) (violet). The reason is that the electron and hole energy levels equivalent to conduction and valence band are more tilted due to the influence of the low conductivity. Rod MacKenzie from Durham used his drift–diffusion simulation programme gpvdm – which among many other features allows to use the multiple-trapping-and-release model to account for energetic disorder – to calculate an example. In the figure, the energy levels corresponding to conduction and valence band are shown, and the yellow shading between the band edges correspond to the trap populations which I will ignore. So focus on the edges! 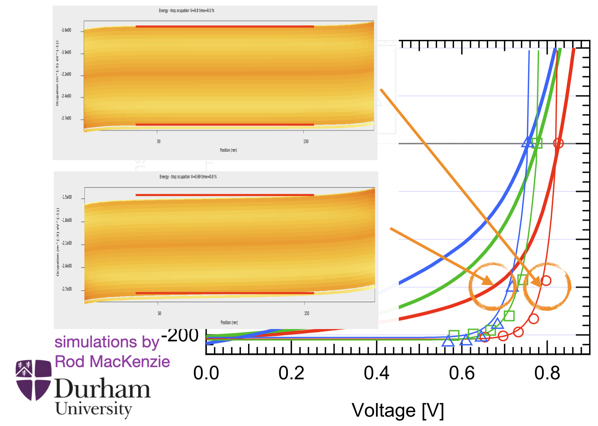Band bending due to transport resistance, by Rod MacKenzie using gpvdm The upper left inset features the band bending of the transport resistance free case at a current–voltage point in the fourth quadrant of an illuminated solar cell, V_\text{int} being at 0.8 V. The red lines show that in the bulk, the bands are perfectly flat despite not being at any “flat band” voltage. In contrast, the lower left inset shows the band bending for the illuminated current–voltage point at the same current, but at V_\text{ext} of 0.69 V. The voltage difference \Delta V of 0.11 V is due to the transport resistance. The two perfectly horizontal red lines, just shifted down from above, now show a discrepancy due to the band bending in the bulk. This tilt sums up to the voltage loss \Delta V, and corresponds to a gradient of the quasi-Fermi levels, as discussed clearly in [Würfel/Neher et al 2015] around Eqn (8). Let me note that the denomination of V_\text{int} as opposed to V_\text{ext} is a bit unfair, as the latter still drops across the whole (active) layer thickness L – but the gradient is different. So, can the two different band bendings (upper left and upper right) occur at the same time? No of course not. The lower right shows you how a simulated organic solar cell with realistic parameters looks inside: it is limited by a transport resistance due to low effective conductivity in the active layer, which shows up as tilt in the bands, and implies a gradient in the quasi-Fermi levels. The upper right shows you how the bands looked if the solar cell were not limited by a transport resistance (and how they do look under the special case of open circuit conditions).

Still, the voltage drop due to the transport resistance – coming from the low conductivity and leading to the tilted transport levels – is real and does reduce the fill factor.

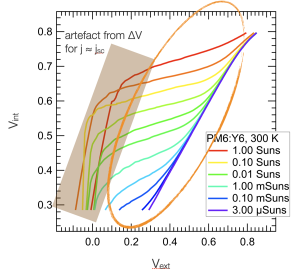In my recent talk at the MRS Spring meeting (invited! in person! on Hawaii! slides here:), I showed the approximate difference of the internal and external voltage of a fresh, inverted PM6:Y6 bulk heterojunction solar cell (L = 200 nm, but qualitatively similar for 100 nm) at different light intensities, from 3 micro-suns to 1 sun (300 nW/cm2 to 100 mW/cm2). Sa Vint vs Vext The ideal diagonal case where V_\text{int}=V_\text{ext} is only seen for the lowest light intensities. In contrast, at 1 sun illumination, when 0.4 V are applied, the internal voltage is still at around 0.7 V. The fill factor at 1 sun is, by the way, somewhat above 60%, whereas the transport resistance free pseudo fill factor (determined using the Suns-Voc method, see below) is above 80%. As If you are interested in the details of this study, please have a look at our preprint. [Update 2022-07-01]: now published in Nature Communications.

How did we determine the approximate internal voltage, or j(V_\text{int}), when we only have direct access to the external (i.e., applied) voltage? Similar to [Schiefer et al 2014], we used the Suns-Voc method as a measure for the series and transport resistance free current–voltage characteristics. The idea is in the post on the diode ideality factor, but before sending you away again I repeat it here: the current density, as given by the diode equation under assumption of the superposition principle,

j = j_0 \left( \exp\left(\frac{q(V_\text{ext}-jR_s)}{nkT} \right) -1 \right) - \frac{V_\text{ext}-jR_s}{R_p} - j_\text{gen} (*)

is influenced by the series resistance R_s and parallel resistance R_p. At open circuit, V_\text{ext} = V_\text{int} = V_{oc}, the current j(V_{oc}) is zero,

0 = j_0 \left( \exp\left(\frac{q(V_{oc}-0 R_s)}{nkT} \right) -1 \right) - \frac{V_{oc}- 0 R_s}{R_p} - j_\text{gen},

so that the terms including the series resistance (but not the parallel resistance!) become zero as well. Reordering the equation,

j_\text{gen} = j_0 \left( \exp\left(\frac{qV_{oc}}{nkT} \right) -1 \right) - \frac{V_{oc}}{R_p},

we have an equation very similar to the diode equation (*). The pairs j_\text{gen}(V_{oc}) measured under a wide range of light intensities can, when shifted down by j_{sc}(\text{1 sun}), correspond to the so called Suns-Voc curve. It represents the j(V_\text{int}) curve, as the open circuit voltage is transport resistance free so that (only) there, \Delta V=0. The Suns-Voc curve is equivalent to the illuminated j(V_\text{ext}) curve, but lacks the influence of the series and transport resistance. The generation current j_\text{gen} \approx eGL with the generation rate G is sometimes (ok, often..) approximated by the short circuit current j_{sc}.
An example of how a Suns-Voc curve looks is shown in my earlier post on the diode ideality factor in the third figure (red = illuminated j(V_\text{ext}), green symbols = Suns-Voc curve).

Of course there is a better way by measuring both the voltage dependent current and luminescence of a solar cell, as done by [Rau et al 2020] on Cu(In,Ga)Se2 solar cells: from the luminescence, which depends on the quasi-Fermi level splitting, the internal voltage can be determined. For organic solar cells, as singlet and charge transfer exciton photoluminescence need to be separated – the internal voltage will be proportional to the latter – this is harder and has not been done yet, as far as I know.

How can the impact of the transport resistance on the fill factor, and thus performance, of organic solar cells be minimised? To reduce the transport resistance, the active layer conductivity needs to be increased. This can be done by, either, increasing the charge carrier mobility – for a molecular hopping system this means reducing static (low \sigma) and/or dynamic disorder (low \lambda). Or, increasing the carrier concentration – e.g. by doping, which is kind of hard in a bulk heterojunction, but starting with the material phase with the lower conductivity could be a viable approach.

Some hat tips here beyond the very nice cooperation of our study: Maria and Rod for feedback to an earlier version of the post, and Julien for being the first commenter on it:)